Least Squares Regression

Line of Best Fit

Imagine you have some points, and want to have aline that best fits them like this:

scatter plot ice cream vs temp with line

We can place the line "by eye": try to have the line as close as possible to all points, and a similar number of points above and below the line.

But for better accuracy let's see how to calculate the line using Least Squares Regression.

The Line

Our aim is to calculate the values m (slope) and b (y-intercept) in the equation of a line :

Where:

  • y = how far up
  • x = how far along
  • m = Slope or Gradient (how steep the line is)
  • b = the Y Intercept (where the line crosses the Y axis)

Steps

To find the line of best fit for N points:

Step 1: For each (x,y) point calculate x2 and xy

Step 2: Sum all x, y, x2 and xy, which gives us Σx, Σy, Σx2 and Σxy (Σ means "sum up")

Step 3: Calculate Slope m:

m = N Σ(xy) − Σx Σy N Σ(x2) − (Σx)2

(N is the number of points.)

Step 4: Calculate Intercept b:

b = Σy − m Σx N

Step 5: Assemble the equation of a line

y = mx + b

Done!

Example

Let's have an example to see how to do it!

ice cream

Example: Sam found how many hours of sunshine vs how many ice creams were sold at the shop from Monday to Friday:

"x"
Hours of Sunshine		 "y"
Ice Creams Sold
2 4
3 5
5 7
7 10
9 15

Let us find the best m (slope) and b (y-intercept) that suits that data

y = mx + b

Step 1: For each (x,y) calculate x2 and xy:

x y x2 xy
2 4 4 8
3 5 9 15
5 7 25 35
7 10 49 70
9 15 81 135

Step 2: Sum x, y, x2 and xy (gives us Σx, Σy, Σx2 and Σxy):

x y x2 xy
2 4 4 8
3 5 9 15
5 7 25 35
7 10 49 70
9 15 81 135
Σx: 26 Σy: 41 Σx2: 168 Σxy: 263

Also N (number of data values) = 5

Step 3: Calculate Slope m:

m = N Σ(xy) − Σx Σy N Σ(x2) − (Σx)2

= 5 x 263 − 26 x 41 5 x 168 − 262

= 1315 − 1066 840 − 676

= 249 164 = 1.5183...

Step 4: Calculate Intercept b:

b = Σy − m Σx N

= 41 − 1.5183 x 26 5

= 0.3049...

Step 5: Assemble the equation of a line:

y = mx + b

y = 1.518x + 0.305

Let's see how it works out:

x y y = 1.518x + 0.305 error
2 4 3.34 −0.66
3 5 4.86 −0.14
5 7 7.89 0.89
7 10 10.93 0.93
9 15 13.97 −1.03

Here are the (x,y) points and the line y = 1.518x + 0.305 on a graph:

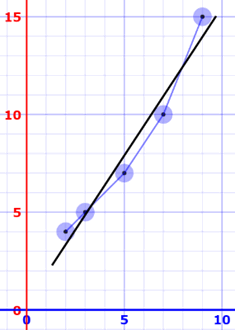
least squares example graph

Nice fit!

Sam hears the weather forecast which says "we expect 8 hours of sun tomorrow", so he uses the above equation to estimate that he will sell

y = 1.518 x 8 + 0.305 = 12.45 Ice Creams

Sam makes fresh waffle cone mixture for 14 ice creams just in case. Yum.

How does it work?

It works by making the total of the square of the errors as small as possible (that is why it is called "least squares"):

least squares example graph
The straight line minimizes the sum of squared errors

So, when we square each of those errors and add them all up, the total is as small as possible.

You can imagine (but not accurately) each data point connected to a straight bar by springs:

least squares example graph
Boing!

Outliers

Be careful! Least squares is sensitive to outliers. A strange value will pull the line towards it.

Use the App

Have a play with the Least Squares Calculator

Not Just For Lines

This idea can be used in many other areas, not just lines.

least squares circle graph
A "circle of best fit"

But the formulas (and the steps taken) will be very different!